題目
Given a 2D matrix matrix, handle multiple queries of the following type:
- Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
Implement the NumMatrix class:
- NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
- int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
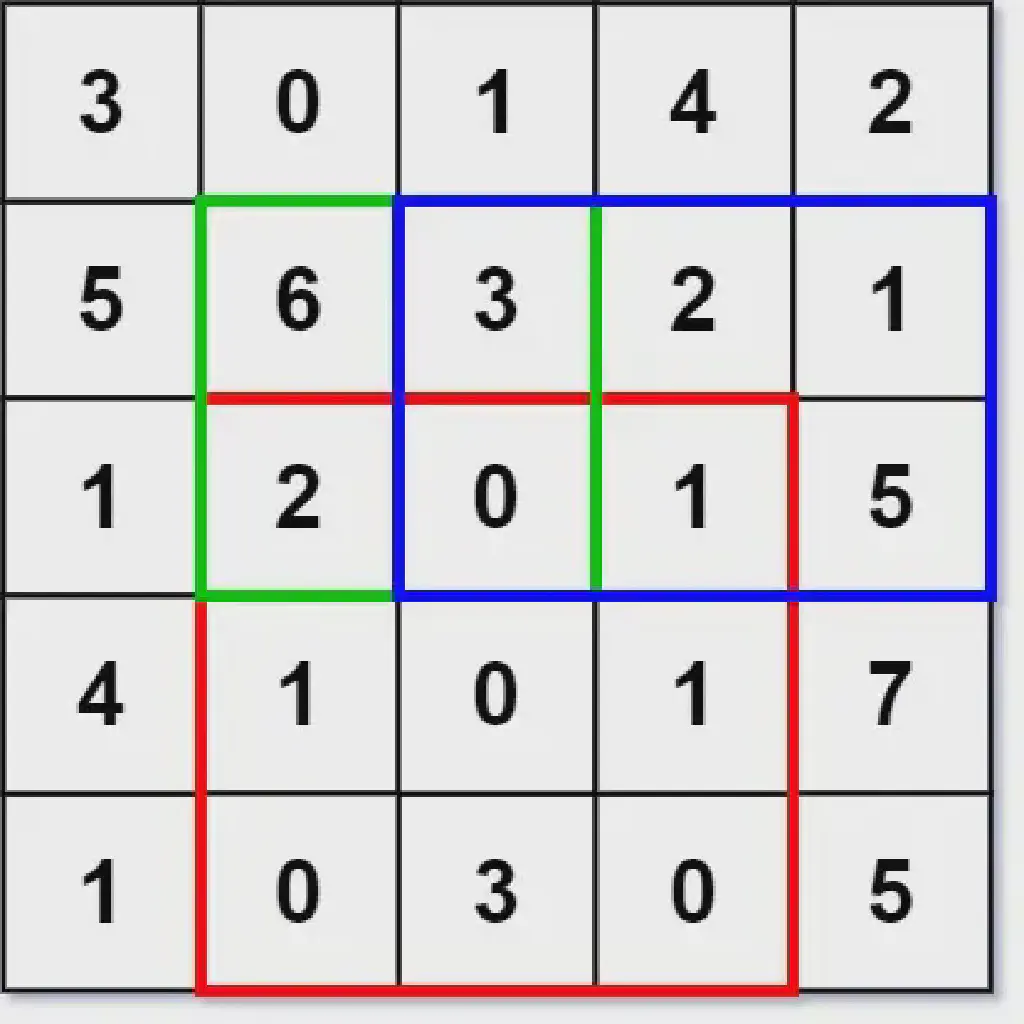
Example:
1Input
2["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
3[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
4Output
5[null, 8, 11, 12]
6
7Explanation
8NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
9numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
10numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
11numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
Constraints:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 200
- -104 <= matrix[i][j] <= 104
- 0 <= row1 <= row2 < m
- 0 <= col1 <= col2 < n
- At most 104 calls will be made to sumRegion.
我的思路
由於提供了 row1, row2, col1, col2,每次 call sumRegion 的時候,loop 一遍將所有的數字加起來
程式碼
1class NumMatrix {
2 int[][] matrix;
3
4 public NumMatrix(int[][] matrix) {
5 this.matrix = matrix;
6 }
7
8 public int sumRegion(int row1, int col1, int row2, int col2) {
9 int sum = 0;
10 for(int row = row1; row <= row2; row++) {
11 for(int col = col1; col <= col2; col++) {
12 sum += matrix[row][col];
13 }
14 }
15 return sum;
16 }
17}
我的思路2
由於從範例可以看到 sumRegion 是在同一個 matrix 重複去計算,所以可以在 call NumMatrix constructor 時事先做一些計算並存起來,以便加快 sumRegion 時的計算。
現在我打算建立 2D Array cache,而 cache[m][n] 代表的是 [0][0] 到 [m][n] 的所有數字的總和。
從下面的圖我們可以看到 cache[d1][d2] = A + B + C + D
如果我們只是想要圖中 D 的面積的話,可以等於
- = (A + B + C + D) - (A + C) - (A + B) + A
- = cache[d1][d2] - cache[c1][c2] - cache[b1][b2] + cache[a1][a2]
![example]example.webp?width=1024px#center)
程式碼2
1class NumMatrix {
2 int[][] cache;
3
4 public NumMatrix(int[][] matrix) {
5 int m = matrix.length;
6 int n = matrix[0].length;
7 cache = new int[m][n];
8 cache[0][0] = matrix[0][0];
9
10 for(int row = 0; row < m; row++) {
11 for(int col = 0; col < n; col++) {
12 if (row == 0 && col ==0) {
13 continue;
14 }
15 if(row == 0) {
16 cache[row][col] = cache[row][col-1] + matrix[row][col];
17 } else if (col == 0) {
18 cache[row][col] = cache[row -1][col] + matrix[row][col];
19 } else {
20 cache[row][col] = cache[row][col -1] + cache[row -1][col] - cache[row -1][col -1] + matrix[row][col];
21 }
22 }
23 }
24 }
25
26 public int sumRegion(int row1, int col1, int row2, int col2) {
27 if (row1 == 0 && col1 == 0) {
28 return cache[row2][col2];
29 } else if (row1 == 0) {
30 return cache[row2][col2] - cache[row2][col1-1];
31 } else if (col1 == 0) {
32 return cache[row2][col2] - cache[row1-1][col2];
33 } else {
34 return cache[row2][col2] - cache[row1-1][col2] - cache[row2][col1-1] + cache[row1-1][col1-1];
35 }
36
37 }
38}
由於不用每次都從頭計算,在 Leetcode上執行的數度是 程式碼1 的 20倍快


評論